The only way to know why is to look at it from a wider perspective. If you think about it, the properties of these fractions only hold for a particular base. If you interpret 16/64 in base 7 you'll find that canceling the 6's will be very, very wrong. And 15/53 certainly does not have this property in base 10 but if interpreted in base 6 the property manifests. This means that given any number for a base, there will be a set (not necessarily non-empty) of fractions with this strange property. I will refer fractions with this property in a particular base b as weird in base b. (I'm not very original.)
But now came the problem of the perspective one should take in looking at the problem. When writing out the fractions, for instance, should you reduce the fractions, or keep them in the form they were found? Should you look at cancellations with 3, 4, or 5 digits or stick to 2? What if a fraction is repeated in 2 different forms? Should you include it twice? Or maybe you should look at the products of the fractions alone, and not worry about what they are individually. In the end, I decided to output them as completely simplified fractions and to only focus on the two digit examples This was for a few reasons
- Reducing the fractions lets me not have to write it in it's original base. I'm focusing on the actual value of the fraction and not the symbols that compose it. Thus, I can write all fractions in the familiar base 10 and not have to worry about notation for bases higher than 10. (For example, writing 15 in base 16 would force me to go past our regular digits and use new symbols. People usually start to use letters after that (making 10 = A, 11 = B...15= F...), but that would only work for up to 36, and I'd want to look at numbers higher than that).
- The products themselves are too little information. Looking at the components of the products allows one to see its origins, what exactly caused the result.
- Two digits are the simplest possible case for this kind of thing. If there is a pattern, it should be easiest to spot there.
So, going off that, in order to study this at all we need a large set of an actual example of these fractions. So, the next step is to find an algorithm that produces the weird fractions for any particular base. For a particular base k we can write a number n as the sum of a series of numbers,
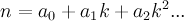
where
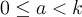 . ai is merely the i-th digit in the base k representation. For example,
. ai is merely the i-th digit in the base k representation. For example, 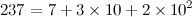 . Thus, we can represent the 2 digit numerators and denominators, of base k, in the form
. Thus, we can represent the 2 digit numerators and denominators, of base k, in the form 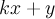 with x and y greater than or equal to 0 and less than k. And since we need a digit to cancel with either x or y should appear twice in the fraction.
with x and y greater than or equal to 0 and less than k. And since we need a digit to cancel with either x or y should appear twice in the fraction.We have to be careful about where we put the repeated digit as that would affect our answer. The weird fractions in base 10, 16/64, 19/95, 26/65, 49/98 all have the cancellations taking place from the right digit of the numerator to he left digit of the denominator. This means that all those fractions are of the form.
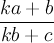
Now, it turns out that all weird fractions less than one in any base k are of this form. You can understand this by looking at the other options. For both cancellations take place on the right digit then either the numerator is equal to the denominator or the digit being cancelled is simply 0, both of which are trivial cases. When both are cancelled from the left, the same conclusions can be drawn. That only leaves the cases where the digits being canceled are across from each other diagonally. When we cancel diagonally from the top left to the bottom right however, the only weird fractions found are greater than one (actually the inverses of the weird fractions less than 1). I'll leave it as an fun little exercise to the reader to figure out why. (Meaning, I really have no idea why.)
Now, if we write the fraction as above we can form the following equation by canceling out the b's.
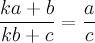
And then problem becomes finding the values of a, b and c that satisfy the equation for a given base k. The easiest way for me to do this was to solve for c (I could have just as easily solved for a or b ) and have the computer iterating through the possible values for a and b (0, 1, ..., k - 1), calculating the value of c at each step. If c turned out to be an integer, we will have found values that form a weird fraction. What's left is to simply calculate a/c and add that to the list of weird fractions for that base.
Using this method, I produced a table for the weird fractions (in simplified form) of every base from 2 to 100. Here are the one's up to 20.
- 2:
- 3:
- 4: 1/2
- 5:
- 6: 1/3 1/2
- 7:
- 8: 1/4 1/2
- 9: 1/3
- 10: 1/5 1/4 2/5 1/2
- 11:
- 12: 1/6 1/4 1/3 1/2
- 13:
- 14: 1/7 1/2
- 15: 1/5 2/9 3/10 1/3
- 16: 1/8 1/6 1/4 3/8 1/2
- 17:
- 18: 1/9 1/6 1/3 1/2
- 19:
- 20: 1/10 1/5 1/4 1/2
So, where does that leave us? Well, as long as we're talking about divisors there is another pattern. The inverses of all divisors of the given base can be found in that set of weird fractions for that base. This, however, does not, in general, produce all the weird fractions for a base. So, the natural thing to ask is, what's up with the fractions that aren't merely inverses of divisors?
This occurs in our very own base 10. The 2/5 and 1/4 just don't fit in with 1/5 and 1/2.Well, I haven't gotten that far yet. But, I must note that in every b's set of weird fractions, if x/y is in that set than y/xb is also in it. That is, every fraction in the set can be multiplied by another fraction (or itself) to produce 1/b. This will certainly lend insight onto where weird fractions come from, and maybe even lead to a simple algorithm for producing them without guess and check.
So, yeah, weird fractions. Cool stuff.