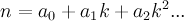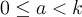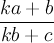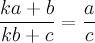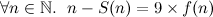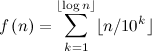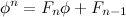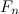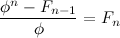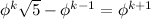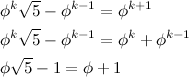Logical Paraodoxes

Paradoxes have always fascinated me. They take seemingly self-evident facts and use them to arrive at ridiculous, surely impossible conclusions. Paradoxes force us to re-evaluate our most basic concepts of the world. We can no longer take even the simplest premises on faith, as when faced with a paradox there is no other possible conclusion that one of our "obvious" assumptions must be wrong. And correcting these assumptions inevitably leads to a better understanding of the universe and new discoveries in mathematics.

The greatest example of this is Zeno's paradox. Zeno was a Greek philosopher in the 5th century B.C. He created several paradoxes, but I'm going to focus on the paradox Achilles and the tortoise. One day, the tortoise challenged Achilles to a race. Achilles, as you know, was a great and powerful Greek warrior. Surely he should have no problem racing a tortoise. But, knowing he is at a disadvantage, the tortoise asks for a head start of 10 meters. Achilles agrees, knowing he could recover from such a small disadvantage with ease. So, the race begins with the tortoise 10 meters ahead, inching along as tortoises do. Achilles bursts from the starting line like a locomotive. He covers the 10 meters in a few seconds. But by the time he does this, the tortoise has moved ahead, though only slightly. No matter. In a brief moment he covers that distance as well. But, in the time it took him to do this, however small, the tortoise has moved ahead still. And by the time he reaches where the tortoise is now, it will have moved ahead again. So it seems that he can never really catch the tortoise, as the tortoise will always be ahead.

This is certainly a baffling result. I mean, no one in his right mind would claim that Achilles would lose to a tortoise. But then, what went wrong? What was wrong with our reasoning? In this case, the heart of the problem lies in dealing with infinite sums. Think about it. It takes Achilles a certain amount of time to run the first 10 meters, and in that time the tortoise will have moved a little bit ahead. It takes Achilles some time to cover the second distance, some time to cover the third distance and so on. Zeno is proposing that since there an infinite amount of periods of time, the total time taken (i.e. the sum) must itself be infinite. The problem with that, as modern mathematics has shown us, that simply isn't true. It turns out that since each period of time is smaller than the previous, it is possible that the sum of all of them is finite. Though, it is not guaranteed that just because the elements of the sum are decreasing, the infinite sum will be finite. See the harmonic series, for example.

To see this in action, let's calculate how long it does take Achilles to reach the tortoise. First off, to make the math easier, let's say the tortoise was only 1 meter ahead and was traveling at 1 m/s and Achilles was traveling at 2 m/s. Achilles covers the first meter in 1/2 a second, but by that time the tortoise has moved 1/2 of a meter ahead of his previous position. Achilles will cover the next 1/2 meter in 1/4 of a second and the tortoise will move ahead 1/4 meter and so on. The periods of time it takes Achilles to cover the distances are 1/2 second, 1/4 second, 1/8 second, 1/16 second, and blah blah blah. So the total time until he passes the tortoise is 1/2 + 1/4 + 1/8... . But what does this sum up to? Let's take it bit by bit. 1/2 + 1/4 = 3/4. And 3/4 + 1/8 = 6/8 + 1/8 = 7/8. And 7/8 + 1/16 = 14/16 + 1/16 = 15/16. I'm sure you see the pattern. The denominator is always a power of two while the numerator is one less. It's obvious that this sum will not go off to infinity. In fact, the sum will never be greater than 1. But it will be getting closer and closer to 1 the more terms we add. Since we can get arbitrarily close to 1 but never exceed it, we can conclude it will take Achilles exactly 1 second to catch up to the tortoise.

And is exactly the concept known as a limit in mathematics. The understanding of limits is central to the formulation of calculus, and, as a result, everything calculus is used for. This is a rather long list, intersecting with every field of science. The solution of this paradox came with the knowledge to create the most revolutionary discovery to have ever existed. But, this is just one, of many paradoxes known today. Several of these have been explained thoroughly, but there are several more that have yet to be solved.

One of the most famous paradoxes today is known as the Liar Paradox. It's been stated in many different forms, but the simplest is probably :

This statement is false.

You can easily see something is wrong here. Is the statement true or false? If we assume it's true, it must be correct in saying that it's false, and, thus, must be false, which is a contradiction. If we assume it's false, we can see it is correct when it says it's false, and must be true, which is also a contradiction.

When I first came across this, I thought it was simple. If it can't be false, and it can't be true, why not just call it neither, or "null"? Easy, right? Then someone made the statement:

This statement is false or null.

Well, this is a problem. If the statement is false, it succumbs to the paradox as the original. And now it can't even be null because then it would actually be true. There is still a contradiction.

So, we should be cautious. We don't know if our "solutions" result in new paradoxes. These things take lots of thought.

There have been a few proposed solutions to this problem, all of which have their merits and shortcomings. I personally haven't reached a conclusion that seems completely satisfactory. None the less, investigating this paradox and paradoxes like these is always a fun experience. Who knows, one may just arrive at indisputable evidence on the inconsistency of logic. (But probably not)

Weird Fractions

I was working on Project Euler problems the other day. Since I hadn't done one in a while, I decided to look up an easy one. I chose Problem 33. Now, the problem itself wasn't difficult to solve. With a few minutes spent programming on my TI-83, I found the fractions satisfying their criteria. The fractions were 16/64, 49/98, 19/95, and 26/65. The final answer, the product of these, left me puzzled,though. Taking the product of all of these you get simply 1/100. Such a queer answer. I expected something complicated like 19/40 or maybe 23/57. But no. Just 1/100. For any critical thinker, the obvious question presents itself. Why?

The only way to know why is to look at it from a wider perspective. If you think about it, the properties of these fractions only hold for a particular base. If you interpret 16/64 in base 7 you'll find that canceling the 6's will be very, very wrong. And 15/53 certainly does not have this property in base 10 but if interpreted in base 6 the property manifests. This means that given any number for a base, there will be a set (not necessarily non-empty) of fractions with this strange property. I will refer fractions with this property in a particular base b as weird in base b. (I'm not very original.)

But now came the problem of the perspective one should take in looking at the problem. When writing out the fractions, for instance, should you reduce the fractions, or keep them in the form they were found? Should you look at cancellations with 3, 4, or 5 digits or stick to 2? What if a fraction is repeated in 2 different forms? Should you include it twice? Or maybe you should look at the products of the fractions alone, and not worry about what they are individually. In the end, I decided to output them as completely simplified fractions and to only focus on the two digit examples This was for a few reasons

1. Reducing the fractions lets me not have to write it in it's original base. I'm focusing on the actual value of the fraction and not the symbols that compose it. Thus, I can write all fractions in the familiar base 10 and not have to worry about notation for bases higher than 10. (For example, writing 15 in base 16 would force me to go past our regular digits and use new symbols. People usually start to use letters after that (making 10 = A, 11 = B...15= F...), but that would only work for up to 36, and I'd want to look at numbers higher than that).
   
2. The products themselves are too little information. Looking at the components of the products allows one to see its origins, what exactly caused the result.
3. Two digits are the simplest possible case for this kind of thing. If there is a pattern, it should be easiest to spot there.
   

Finally, we need a goal. Simply, "understanding weird fractions" seems a bit vague. The way I see it, if we're able to make an algorithm to produce weird fractions without guess-and-check, we should have a pretty good understanding of them. For a full understanding, this algorithm may even be useable for 3 or more digits.


So, going off that, in order to study this at all we need a large set of an actual example of these fractions. So, the next step is to find an algorithm that produces the weird fractions for any particular base. For a particular base k we can write a number n as the sum of a series of numbers,



where . ai is merely the i-th digit in the base k representation. For example, . Thus, we can represent the 2 digit numerators and denominators, of base k, in the form with x and y greater than or equal to 0 and less than k. And since we need a digit to cancel with either x or y should appear twice in the fraction.

We have to be careful about where we put the repeated digit as that would affect our answer. The weird fractions in base 10, 16/64, 19/95, 26/65, 49/98 all have the cancellations taking place from the right digit of the numerator to he left digit of the denominator. This means that all those fractions are of the form.



Now, it turns out that all weird fractions less than one in any base k are of this form. You can understand this by looking at the other options. For both cancellations take place on the right digit then either the numerator is equal to the denominator or the digit being cancelled is simply 0, both of which are trivial cases. When both are cancelled from the left, the same conclusions can be drawn. That only leaves the cases where the digits being canceled are across from each other diagonally. When we cancel diagonally from the top left to the bottom right however, the only weird fractions found are greater than one (actually the inverses of the weird fractions less than 1). I'll leave it as an fun little exercise to the reader to figure out why. (Meaning, I really have no idea why.)


Now, if we write the fraction as above we can form the following equation by canceling out the b's.




And then problem becomes finding the values of a, b and c that satisfy the equation for a given base k. The easiest way for me to do this was to solve for c (I could have just as easily solved for a or b ) and have the computer iterating through the possible values for a and b (0, 1, ..., k - 1), calculating the value of c at each step. If c turned out to be an integer, we will have found values that form a weird fraction. What's left is to simply calculate a/c and add that to the list of weird fractions for that base.

Using this method, I produced a table for the weird fractions (in simplified form) of every base from 2 to 100. Here are the one's up to 20.

• 2:
• 3:
• 4: 1/2
• 5:
• 6: 1/3 1/2
• 7:
• 8: 1/4 1/2
• 9: 1/3
• 10: 1/5 1/4 2/5 1/2
• 11:
• 12: 1/6 1/4 1/3 1/2
• 13:
• 14: 1/7 1/2
• 15: 1/5 2/9 3/10 1/3
• 16: 1/8 1/6 1/4 3/8 1/2
• 17:
• 18: 1/9 1/6 1/3 1/2
• 19:
• 20: 1/10 1/5 1/4 1/2

Now's the fun part. It's time to look for some patterns! If you want, try to see how many solid patterns you can find before reading on. Well, there's one very blatantly obvious pattern sticking up here. All prime numbers don't have any fractions with the weird property. The first question we ask is, well, what separates the prime numbers form all other numbers? They don't have any divisors other than 1 and itself. So, the weird fractions for a base k depend on the divisors of k. Using this as a guide a second pattern, that would normally be harder to spot, becomes easily apparent. The denominators of every weird fraction has at least 1 divisor in common with the base they are found in (not counting 1 and the number itself). This criteria would, obviously leave the prime numbers empty.

So, where does that leave us? Well, as long as we're talking about divisors there is another pattern. The inverses of all divisors of the given base can be found in that set of weird fractions for that base. This, however, does not, in general, produce all the weird fractions for a base. So, the natural thing to ask is, what's up with the fractions that aren't merely inverses of divisors?

This occurs in our very own base 10. The 2/5 and 1/4 just don't fit in with 1/5 and 1/2.Well, I haven't gotten that far yet. But, I must note that in every b's set of weird fractions, if x/y is in that set than y/xb is also in it. That is, every fraction in the set can be multiplied by another fraction (or itself) to produce 1/b. This will certainly lend insight onto where weird fractions come from, and maybe even lead to a simple algorithm for producing them without guess and check.

So, yeah, weird fractions. Cool stuff.

8 balls problem

My friend and I were working on an interesting riddle recently. It's one that I'm sure most people have heard before, and probably didn't have much trouble solving. It goes as follows:

Given 8 balls, each weighing exactly the same except one (which we'll assume is heavier), and a scale, what is the least number of times you must use the scale to find the heavy ball?

The approach most frequently thought of is to split the 8 balls into 2 pairs 4 balls and place those on the scale. Then, go to the side that turns out heavier, and split those 4 balls into 2 pairs of 2 balls and place those on the scale. When one side turns out heavier, weigh those final 2 balls and you'll find the heavy ball.

But as anyone who has ever heard a riddle in his life would know, the most obvious answer is rarely the correct one. You can actually find the heavy ball using the scale only twice. To do this, you must set to balls aside, and weigh the final 6 with 3 on each side of the scale. If they balance, you know the heavy ball is among the final two and you need only weigh those. If they don't, you need only weigh 2 of the final 3, because, if those two balance, we know the heavy one is the final, unweighed ball, if they don't, the heavy ball would obviously be the heavier one of the two.


Pretty simple, yes? But then the question arises. What if you were given 9 balls? Or 20? 81 balls? What will the minimum usage of the scale be then? We worked on this for a bit, and got a table showing the least number of times required to find the heavy ball out of n balls. It started off like

1: 0*
2: 1
3: 1
4: 2
5: 2
6: 2
7: 2
8: 2
9: 2
10: 3

* If you have just one ball, you don't have to weigh anything to figure out it's the heavy ball.

Side Note:

Our table was actually a little bit more expressive. This is because of the fact that, in each case, you have the probability of finding the heavy ball on your first try, your second try, and so on, depending on how you weigh the balls. For example, given 4 balls, you could weigh 2 on each side, and weigh the heavier 2 again, giving you 0 chance of finding it on your first try. Or you could 1 on each side, and only weigh the remaining two if these balance out. But, if they don't balance out, then you'd have found the heavy ball in your first attempt. This post ignores that, as I haven't been able to find anything interesting when including these probabilities. That could be something for a later time.

Do you happen to see a pattern? For 1 ball it takes 0 weighings. For 2-3 balls it takes 1. For 4 - 9 balls it takes 2. Now, it turns out that for 10 - 27 balls it takes 3. I'm sure you've seen it by now. It is indeed a logarithmic growth rate, but of base 3, and not 2. The reason for this? Why, it's simple. While deciding how to weigh the balls one must consider both how many to place on each scale and how many to ignore. The naive method of simply splitting the balls in half and repeating completely disregards the information that can be gained from simply placing to the side a number of balls.

I won't bother at a formal proof that this is the least number of weighings needed to find the heavy ball. (If you don't believe me, you can try to find a more efficient way yourself). I will however, describe a simple method that can be used to find the proper way to weigh a set of "n" balls. You must keep in mind only two things. The number of balls you put on each scale and the number of balls you place aside. Each of these numbers must be less than the greatest power of 3 less than n. (the previous power of three to n.). As long as these criteria are met, you will weigh the balls most efficiently. For example, if given 100 balls, I'm allowed to put up to 81 on each scale (of course, the restraints of the number limit me to putting 50 on each scale), but I also must make sure not to put more than 81 aside. (Technically, I can only put 80 aside. If I put 81 aside, I'm left with 19 balls which I can't divide evenly among the scale).

Well, that's it for today. Hope you found it interesting.

Sum of Digits

This is just an intriguing fact I discovered while doing a project euler problem (number 56 to be specific). The problem asked for the largest sum of digits of any number of the form a^b where both a and b are between 0 and 100. As I often do, I'm going through a rather circuitous path in discovering the answer. While doing this, I happened upon an interesting fact about numbers. If you subtract the sum of the digits of any number, from the number itself, you gain a multiple of nine. That is

Where S(x) obviously denotes the sum of the digits of x. I honestly don't know why this is true just yet. Though, I do know that a similar formula is true for all other bases. That is, for any number n written in base b, if you subtract the sum of the digits of x from I decided to explore this some more. I wanted to see if I could define a function F(x) that defines the exact multiple of nine that results from subtracting the sum of the digits of a number from the number itself. What I mean to say is I want to find a function such that



So, I did some experimenting. I wrote a program that listed the values f(n) should take on from 1 to 100. It turns out that it followed a rather simple pattern.



Though, this probably won't get me any closer to solving the problem, it is something interesting to think about. Just thought I'd share.

My attempt at being Funny.

I was messing around with Macromedia's Flash movie creator recently. I've always been interested in comic making and thought it would be a good chance to try my hand at it. These are my first few attempts at being funny. Now, I don't expect to become the next Randall Munroe (Though, that'd be freakin' awesome), but I'd rather not make horrible comics. So, for all of you reading this (i.e. nobody) I'd be happy to see some criticisms of this work.

They're too large to fit in this screen directly, (and I'm too lazy to shrink them) so I'll just post direct links.

First Comic
Second Comic
Third Comic


Kind of a short post for me, but I don't have anything interesting to post right now. So....yeah. See ya later.

Golden Ratio, Part II

Well, as I said, everything there is to know about the φ couldn't possibly be condensed into a single blog post. Probably wouldn't fit into two either but I figure there was still quite a bit more left to talk about that I didn't get into in the previous post. For starters, I sort of felt bad the proof I showed for the formula to produce Fibonacci numbers wasn't very original. You can find it on Wikipedia on the page for Fibonacci numbers. I thought about it some more, and came up with an alternate, albeit a slightly more complicated, proof. I just wanted to post it up because I thought it was pretty interesting.

Remember the formula for expressing powers of φ in terms of it's first power and a constant, reprinted below:



Rearranging the formula we can place to isolate the variable. Doing, this, we obtain:



Not very helpful so far. But, we can substitute F_(n-1) with a similar expression, repeat this with the F_(n-2) that appears and so on and so on, until Finally we reach F_0, which, as stated before, is equal to 0. The resulting equation will look something like this:




Yeah, still won't be very much use in the proof. It would help if we remove the fractions from the numerator. To do this, we simply multiply by φ / φ exactly n-1 times. (Had to be cautious at this point. A fencepost error would've screwed me over). Also, when subtracting, we must make sure to flip the negative signs to positive ones. When we do this, the resulting expression goes in a + then - pattern. When all is said and done, we obtain the following formula:


.

There is +/- sign is on the φ term is because in the cases where n is an odd number, it ends up being +φ at the end, but in cases where n is an even number, it ends up being -φ. (i.e., if n was 3, it would go φ^5 - φ^3 + φ, but if n was 4 it'd be φ^7 - φ^5 + φ^3 - φ). I just thought this formula was an intriguing one. Even more interesting is how it's equivalent to the previous one even though that's not obvious at all.

But, how do we prove this equivalence? We could equate it to (φ^n - (1-φ)^n)/sqrt(5) and use identities of \phi to make both expressions the same, but that would most likely end in a lot of headache and frustration (take my word for it). Instead, we could describe the left-hand expression as a series indexed by n. The series would correspond directly to the Fibonacci series, so if we can prove that (φ^n - (1-φ)^n)/sqrt(5) represents

The Series will be defined like this:



For example (using the next to last equation)


Which is what we were aiming for. All that remains is to prove that the formula describes this series. We do this through induction.

It is obviously true for the first element of the series.


Now, for the induction step. That is, proving:

.

Next, we muse the fact that (1-φ) = (-1/φ). We multiply by (1/φ) on the numerator and the denominator.



.

They are looking quite similar at this point. Now, all that's left to do is prove that . This can be done simply, and easily in a few steps.



Plugging in the actual value of φ will show the final statement to be true, thus proving the equivalence of the two formulas.

And there you have it. I don't think I've seen this proof anywhere else on the internet. I'd say it's inferior to the other one, though, because you have to know the end result in order to complete the proof. Though, it did yield an interesting expression that the other proof didn't. That's probably the only superior part.

PS:
If you're wondering about all the different font for the formulas, it's because I switched between using a program called MathType and this website http://mathurl.com/. I then went back and tried to change all the functions to use the website. Stopped caring, and left off with this mess.

Yeah.

Golden Ratio

The golden ratio is a truly remarkable mathematical constant. While, it's not quite as famous or important as π or e, there's still a wealth of information to be discovered from studying it.



For any two numbers a and b that satisfy the equation. That is, the ratio of the a + b to a is equal to the ratio of a to b. To find the exact value of φ we use the fact that (a/b) = φ, meaning a = bφ. Substituting in the first equation gives



And solving for the positive solution yields

.

(Approximated).


One of the coolest thing's about φ is it's relation to the Fibonacci series. The Fibonacci series begins with 1, and the next term is determined by the sum of the previous two terms. The first 10 terms of the series are

1, 1, 2, 3, 5, 8, 13, 21, 34, 55...

So, you get the idea. The explicit definition of the Fibonacci series is below:



The first relationship that comes to mind is seen when you look at the following table

F(n) / F(n-1)	Value	Difference From φ
1/1	1	.618
2/1	2	-0.381
3/2	1.5	0.118
5/3	1.6667	-0.048
8/5	1.6	0.0180
13/8	1.625	-0.0070
21/13	1.6154	0.0026
34/21	1.6190	-0.00101
55/34	1.6176	0.000386
89/55	1.6182	-0.000148

As you can see, the ratio between the consecutive terms of the Fibonacci series approaches φ. This is only the beginning of the relationships these two mathematical phenomena share.

Now, comes the interesting part. Look back at the quadratic we used to calculate the value of &phi. Leave the squared term on the left-hand side of the equation and move the other two terms to the right-side. Now, if we multiply both sides of the equation by φ once, we have φ^3 = φ^2 + φ. If we multiply by φ again we have φ^4 = φ^3 + φ^2. Obviously, since we can multiply by φ any number of times, the following equation is valid.



The recursive nature of this equation leads tho the conclusion that any power of φ can be represented in terms of it's first power and another number. For example, φ^3 is equal to φ^2 + φ, but φ^2 is equal to φ + 1, so φ^3 = 2φ + 1. Any power of φ will go through a similar process until it's eventually expressed in terms of the first power of φ and a constant. The interesting part is the pattern that emerges as you express powers of φ in terms of it's first power.

φ^1 = φ
φ^2 = φ + 1.
φ^3 = φ^2 + φ = (φ + 1) + φ = 2φ + 1
φ^4 = φ^3 + φ^2 = (2φ + 1) + φ +1 = 3φ + 2
φ^5 = φ^4 + φ^3 = (3φ + 2) + (2φ +1) = 5φ + 3.


Observe the coefficients of φ. In order, they go 1, 1, 2, 3, 5. Recognize the pattern? If you don't, I'll give you a hint. It starts with 'F' and ends with 'ibonacci'. That's right! The coefficients of the φ-terms follow the Fibonacci series. That's not all. If you observe the constant term as well, you find that it follows the same pattern, only offset by a single index.



It's relationship with the Fibonacci series doesn't end there. Due to the fact that the formula for calculating the powers of φ is very similar to the formula for determining terms of the Fibonacci series, we can actually use φ to calculate any term of the series we want without bothering to generate the entire series up to that number. The formula to do this is as follows:



It's not immediately obvious where this came from. Though, the proof for it is really quite simple. Before beginning, you should note that φ only refers to the positive solution to the quadratic. The negative solution is simply ignored. But, notice that the negative solution to the quadratic also satisfies the relationship between it's powers that φ does. That is, it's nth power is equal to the sum of the (n-1)th power and the (n-2)th power. Notice also, that the second solution to the quadratic is equivalent to 1 - φ, because:



(Now you know where the (1-φ) came from.)

Now comes the proof. Let's take two real numbers, a and b, and form the expression .aφ^n + b(1-φ)^n. Because of the properties of φ and (1-φ), the value of the expression follows the patterns from before. That is, if we form a series by starting with n = 1, and incrementing n by one each time, it's value at n = k is equal to it's to the sum of it's value at n = k-1 and n = k-2. This can be proven through substitution from the formulas we already have.



Because of this, if this, if we have a function G(n) = aφ^n + b(1-φ)^n, we have the fact that G(n) = G(n-1) + G(n-2). Exactly like the Fibonacci series. Now, all that's left to do is make sure that it begins the same way as the Fibonacci series and the rest of the terms will follow automatically. That is, we must substitute values for a and b so it starts the same way as the series. We do this with a system of equations, using the first two terms of the series. (We could actually use any two terms, but that would make things unnecessarily complicated). Now, we could use the 1st, and 2nd term (1 and 1) but things are even simpler if we use the 0th term and the 1st term. Intuitively, the 0th term should be equal to 0, because 0 + 1 = 1 (the second term.). Now, we obtain the equations




Upon solving, we find



Substituting these values in aφ^n + b(1-φ)^n we obtain the formula we set out to prove.

~Q.E.D.


While this formula is great and all, it leaves a little to be desired. What if you had the problem of finding the first Fibonacci number to be over 1000? Or even determining whether or not a certain number is a Fibonacci number? This formula would be insufficient.


Look back at the formula for generating a Fibonacci number. We can re-express it as


We can use the fact (1-φ)^n / sqrt(5) is always less than one half (you can observe this yourself by punching a few values in your calculator), meaning, that the nth Fibonacci number is the number closets to φ^n / sqrt(5). That is, you plug in φ^n / sqrt(5) and merely round it to the nearest number. This is a very useful formula. Like answering the question from below. What is the first Fibonacci number over 1000? Now, it becomes a rather simple process:




You can use the change of base formula to solve for n. Since n is the point at which φ^n / sqrt(5) becomes 1000 we merely need to take the first integer greater than n and plug it into the equation for finding Fibonacci numbers. Easy peasy lemon squeasy.


Well, that's it for now. It's some pretty cool stuff. Also, for those of you that frequent Project Euler, you could use the final expression discussed here (φ^n / sqrt(5)) to solve Problem 25 with a few calculations on a scientific calculator. It's really quite epic.