Golden Ratio, Part II

Well, as I said, everything there is to know about the φ couldn't possibly be condensed into a single blog post. Probably wouldn't fit into two either but I figure there was still quite a bit more left to talk about that I didn't get into in the previous post. For starters, I sort of felt bad the proof I showed for the formula to produce Fibonacci numbers wasn't very original. You can find it on Wikipedia on the page for Fibonacci numbers. I thought about it some more, and came up with an alternate, albeit a slightly more complicated, proof. I just wanted to post it up because I thought it was pretty interesting.

Remember the formula for expressing powers of φ in terms of it's first power and a constant, reprinted below:



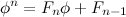
Rearranging the formula we can place to isolate the 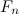variable. Doing, this, we obtain: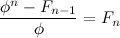



Not very helpful so far. But, we can substitute F_(n-1) with a similar expression, repeat this with the F_(n-2) that appears and so on and so on, until Finally we reach F_0, which, as stated before, is equal to 0. The resulting equation will look something like this:




Yeah, still won't be very much use in the proof. It would help if we remove the fractions from the numerator. To do this, we simply multiply by φ / φ exactly n-1 times. (Had to be cautious at this point. A fencepost error would've screwed me over). Also, when subtracting, we must make sure to flip the negative signs to positive ones. When we do this, the resulting expression goes in a + then - pattern. When all is said and done, we obtain the following formula:


.

There is +/- sign is on the φ term is because in the cases where n is an odd number, it ends up being +φ at the end, but in cases where n is an even number, it ends up being -φ. (i.e., if n was 3, it would go φ^5 - φ^3 + φ, but if n was 4 it'd be φ^7 - φ^5 + φ^3 - φ). I just thought this formula was an intriguing one. Even more interesting is how it's equivalent to the previous one even though that's not obvious at all.

But, how do we prove this equivalence? We could equate it to (φ^n - (1-φ)^n)/sqrt(5) and use identities of \phi to make both expressions the same, but that would most likely end in a lot of headache and frustration (take my word for it). Instead, we could describe the left-hand expression as a series indexed by n. The series would correspond directly to the Fibonacci series, so if we can prove that (φ^n - (1-φ)^n)/sqrt(5) represents

The Series will be defined like this:



For example (using the next to last equation)


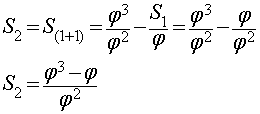
Which is what we were aiming for. All that remains is to prove that the formula describes this series. We do this through induction.

It is obviously true for the first element of the series.


Now, for the induction step. That is, proving:

.

Next, we muse the fact that (1-φ) = (-1/φ). We multiply by (1/φ) on the numerator and the denominator.



.

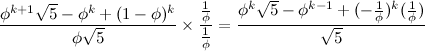
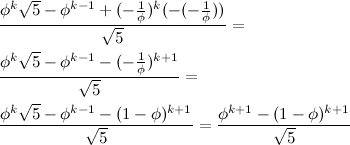They are looking quite similar at this point. Now, all that's left to do is prove that 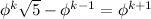. This can be done simply, and easily in a few steps.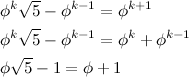



Plugging in the actual value of φ will show the final statement to be true, thus proving the equivalence of the two formulas.

And there you have it. I don't think I've seen this proof anywhere else on the internet. I'd say it's inferior to the other one, though, because you have to know the end result in order to complete the proof. Though, it did yield an interesting expression that the other proof didn't. That's probably the only superior part.

PS:
If you're wondering about all the different font for the formulas, it's because I switched between using a program called MathType and this website http://mathurl.com/. I then went back and tried to change all the functions to use the website. Stopped caring, and left off with this mess.

Yeah.