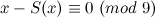
Where S(x) obviously denotes the sum of the digits of x. I honestly don't know why this is true just yet. Though, I do know that a similar formula is true for all other bases. That is, for any number n written in base b, if you subtract the sum of the digits of x from I decided to explore this some more. I wanted to see if I could define a function F(x) that defines the exact multiple of nine that results from subtracting the sum of the digits of a number from the number itself. What I mean to say is I want to find a function
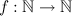such that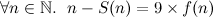
So, I did some experimenting. I wrote a program that listed the values f(n) should take on from 1 to 100. It turns out that it followed a rather simple pattern.
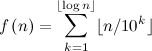
Though, this probably won't get me any closer to solving the problem, it is something interesting to think about. Just thought I'd share.
"If you subtract the sum of the digits of any number, from the number itself, you gain a multiple of nine. I honestly don't know why this is true just yet."
ReplyDeleteActually this is quite easy. It can be reformulated to x is congruent with the sum of digits of x modulo 9.
To see that this holds consider the case when 9 divides x. The sum of digits should be congruent to 0, modulo 9. This can be proven inductivly by taking x=9*n, and base case n=1.
For other x, there will be a y such that floor(x/10)=floor(y/10) and y is a multiple of 9. Since x and y only differ in the least significant digit the difference between the sum of digits will be equal to the difference of x and y. QED.
Ah, yes. I wrote this a while ago, before I realized that fact. But thank you for the comment.
ReplyDeleteWell, my way of thinking about that is the following. If a number x is written in base b, then it's of the form
ReplyDeletex=a_n*b^n+a_{n-1}*b^{n-1}+...+a_2*b^2+a_1*b+a_0.
Then, obviusly the sum of its digits in base b
S_b(x)=a_n+...+a_0.
and if you subtract this from your x you get
x-S_b(x)=a_n*(b^n-1)+...+a_2*(b^2-1)+a_1*(b-1).
Clearly b-1 divides each term of the form b^k-1, since
(b-1)*(b^{k-1}+b^{k-2}+...+b+1)=b^k-1.
Therefore b-1 divides x-S_b(x). In particular for b=10, we get that 9 divides x-S_10(x).